When Marčenko-Pastur meets Bures-Wasserstein
Wishart matrix
The study of empirical covariance matrices dates back to the work of John Wishart [1]. Let \((x^{(n)})_{n\in\mathbb{N}}\) be i.i.d. samples from an underlying distribution, the empirical covariance matrices is given by
\[\Sigma_n = \frac{1}{n}X_n X_n^\top, \quad X_n = \begin{bmatrix} x^{(1)} & \dots & x^{(n)}\\ \end{bmatrix}.\]For simplicity, let us always consider the underlying distribution to be the standard Gaussian \(\mathcal N(0,I)\). Then by our favorite law of large number, \(\Sigma_n\) converges to \(I\).
Marčenko-Pastur distribution
This above convergence surprisingly fails in the high-dimension setting when \(d = n\) (or more generally \(d/n \to \lambda\) but we take \(\lambda = 1\) for simplicity). Marčenko and Pastur proved a limiting spectral distribution in their seminal paper [2]. Let us consider the empirical spectral distribution
\[\eta_n = \frac{1}{n}\sum_{i=1}^{n}\delta_{\lambda_n}\]where \((\lambda_i)_{i=1}^n\) are eigenvalues of \(\Sigma_n\). Then \(\eta_n\) converges weakly to \(\mathrm{MP}\), known as the Marčenko-Pastur distribution. In our simple case, the Marčenko-Pastur distribution \(\mathrm{MP}\) has density
\[f(x) = \frac{1}{2\pi x} \sqrt{(4-x)x}\]supported on \([0,4]\) (see density of general Marčenko-Pastur distribution \(\mathrm{MP}(\lambda, \sigma^2)\) on Wiki). This is not only mathematically beautiful but also demonstrate why empirical spectral could be misleading in high-dimension regime.
Bures-Wasserstein
Let’s set the beautiful random matrix theory aside for now and view \(\Sigma_n\) in the space of positive semidefinite matrix \(\mathcal{S}^n_{+}\). For any \(A, B \in \mathcal{S}^n_{+}\), one may consider \(\mu\sim \mathcal N(A)\) and \(\nu \sim \mathcal N(B)\) be centered Gaussian distributions with covariances \(A\) and \(B\) respectively. Recall that the Wasserstein-2 distance between any two distributions \(\mu, \nu \in \mathcal P(\mathbb R^d)\) is defined by
\[\mathcal W_2^2(\mu,\nu) = \inf_{X\sim \mu, Y\sim \nu} \mathbb E[\Vert X - Y\Vert^2].\]The quadratic cost aligns naturally with the covariance structure of Gaussian measures, which leads to a closed-form expression for the Wasserstein-2 distance between Gaussian distributions given by
\[\mathcal W_2^2(\mu, \nu) = \mathrm{tr}(A + B - 2(A^{1/2}BA^{1/2})^{1/2}).\]Since every centered Gaussian distribution is uniquely determined by its covariance matrix, \(\mathcal W_2\) on Gaussians induce a distance on \(\mathcal{S}^n_{+}\) such that \(d_{\mathrm{BW}}(A,B) = \mathcal W_2(\mu,\nu)\), and the distance is known as the Bures-Wasserstein distance. It turns out that \(\mathcal{S}^n_{+}\) equipped with the \(d_{\mathrm{BW}}\) carries a natural Riemannian manifold structure. We refer the interested reader to [3] for a detailed account of this geometry. For now, we go back to our Wishart matrices.
Bures-Wasserstein distance of Wishart matrix
Now, we can view \(\Sigma_n\) in the space \((\mathcal{S}^n_{+}, d_{\mathrm{BW}})\). It is naturally to ask what is the Bures-Wasserstein distance between \(\Sigma_n\) and \(I\)? Does it also converges to some number as \(n\) goes to infinity? Note that by the close form above, we have
\[\frac{1}{n}d^2_{\mathrm{BW}}(\Sigma_n, I) = \frac{1}{n}\mathrm{tr}(\Sigma_n + I - 2\Sigma_n^{1/2})\]So, we only need to know the limit spectral of \(\Sigma_n\), which is already given by the Marčenko-Pastur distribution above. After some calculation:
\[\frac{1}{n}\mathrm{tr}(\Sigma_n + I) \to \mathbb E_{\Lambda\sim \mathrm{MP}}[\Lambda] + 1 = 2,\] \[\frac{1}{n}\mathrm{tr}(\Sigma_n^{1/2}) \to \mathbb E_{\Lambda\sim \mathrm{MP}}[\sqrt{\Lambda}] = \int_0^4 \sqrt{x}\frac{1}{2\pi x} \sqrt{(4-x)x} \, dx = \frac{8}{3\pi},\]we obtain that
\[\lim_{n \to \infty} \frac{1}{n}d^2_{\mathrm{BW}}(\Sigma_n, I) = \lim_{n \to \infty} \frac{1}{n}\mathrm{tr}(\Sigma_n + I - 2\Sigma_n^{1/2}) = 2(1-\frac{8}{3\pi})\]Finally, we test it numerically and witness the desired convergence.
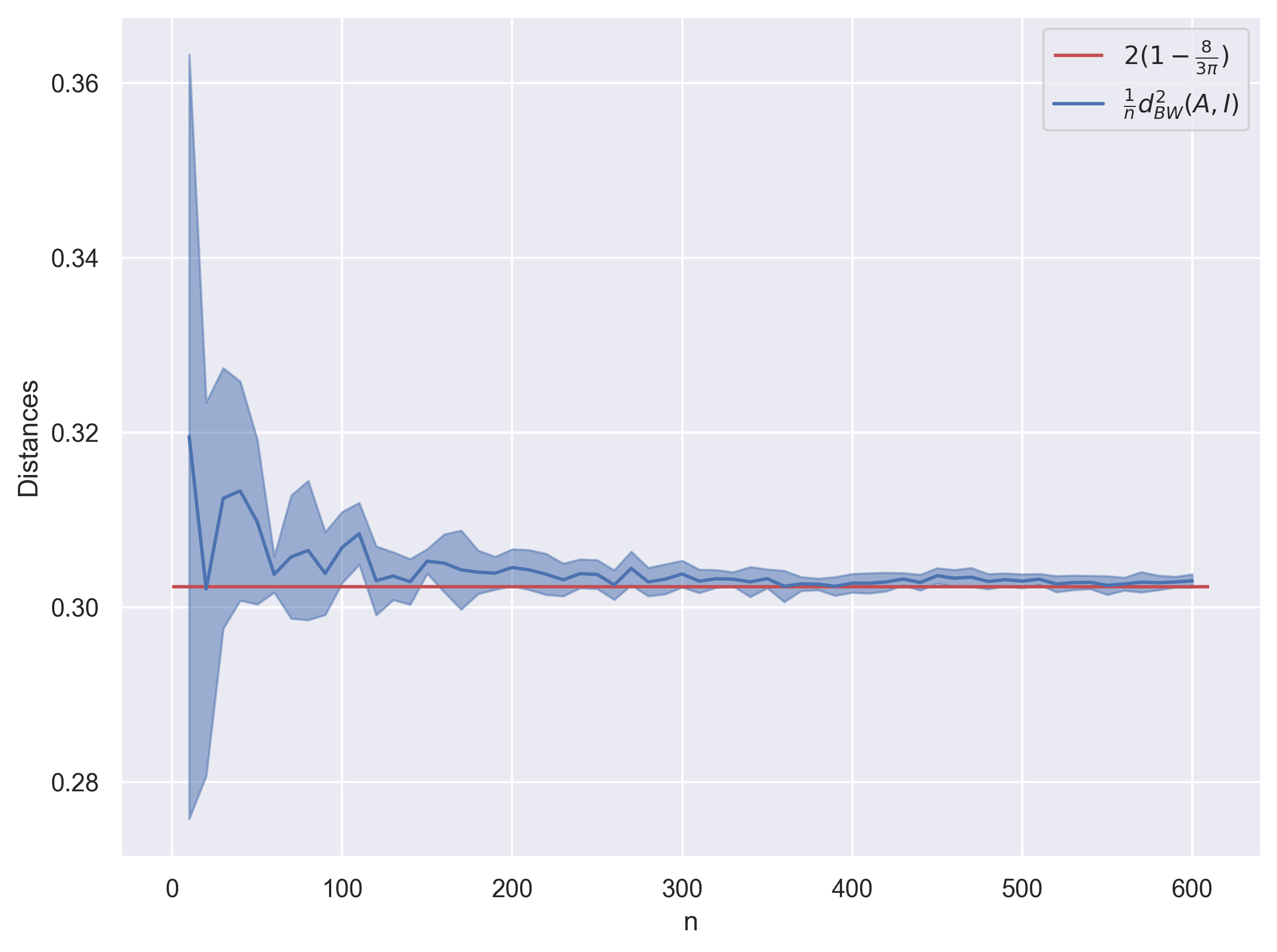
Hope you also find this result cute! I am currently working on this, so if you are interested in this, please feel free to reach out and I would be delighted to discuss.
Reference
[1] Wishart, John. “The generalised product moment distribution in samples from a normal multivariate population.” Biometrika 20.1/2 (1928): 32-52.
[2] Marčenko, Vladimir A., and Leonid Andreevich Pastur. “Distribution of eigenvalues for some sets of random matrices.” Mathematics of the USSR-Sbornik 1.4 (1967): 457.
[3] Takatsu, Asuka. “On Wasserstein geometry of Gaussian measures.” Probabilistic approach to geometry 57 (2010): 463-472.